This article is going to discuss something most may groan at, and that is trigonometry. Before you dismiss this article, you may be suprised at how simple and how fluid trignometry is. Once you get past the “Ugh Math!” part, you will see how essential and useful trignometry is.
Why Study Trig?
You may be wondering why in the world are we studying trigonometry? Where in building a go kart would we need to worry about trigonometry?
Actually trigonometry is very useful for developing various links and dimensions which are relatively difficult to assess or measure. If you’re thinking about developing your own suspension system trigonometry is essential. If you’re thinking about developing a linkage system for a hand crank or some other mechanism, trigonometry is indispensable again.
What is trigonometry? Trigonometry in short is the study of triangles and the relationship between the angles and the sides of the triangle.
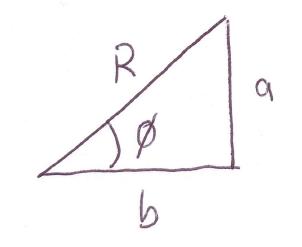
Right Triangle, sides a, b, R and anle Theta
The various links of the sides can be related by sine, cosine and tangent functions. Each one of these three different functions relates to the triangle and can give you a stab at a solution from three different directions.
To start lets lay down the ground rules about trigonometry. First, trigonometric functions are designed around right triangles. More complex obtuse and so forth triangles can be analyzed, however the right triangle is the one were going to study today.
Observe the right triangle with sides A, B. and R.
A lies vertical and B lies horizontal. R is the long side of the triangle. The angle between R and B is the principal angle or Theta.
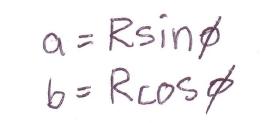 We all know Pythagoreans thereom which says: A squared + B. squared = R squared. (a^2+b^2 = R^2) This provides relationship between A, B and R.
We all know Pythagoreans thereom which says: A squared + B. squared = R squared. (a^2+b^2 = R^2) This provides relationship between A, B and R.
Well with trigonometry the relationship between A and R is as follows:
A = R Sin Theta
and the relationship between B and R is as follows:
B = R Cos Theta
And finally, the relationship between A and B is simply a ratio:
A/B = R Sin Theta/R Cos Theta
Because there are R’s in the numerator in the denominator they cancel:
A/B = Sin theta/Cos theta
Or simply
A/B = Tan Theta

The tangent (Tan) is the ratio of the vertical side divided by the horizontal side.

Triangle Functions
To keep things straight in your head the cosine applies to the horizontal and the sine applies to the vertical side of the triangle.
As you may have observed sine is shortened to sin and cosine is shortened to cos and and finally tangent is simplified to tan.
Basically what we have observed is a simple relationship between the sides of the triangle. The rest of trigonometry invests itself in playing mental gymnastics with the rest of the functions and looking at all different variables associated with them.
The relationship for example between Pythagoras thereom and trigonometry turns out to be a combination of cosines, sines and tangents.

Pythegorem’s Theorem
The identity for example sin squared = 1- cosine squared is an identity that derives itself from the Pythagoras’s theorem.
The way this is accomplished is to view the sides of the triangle as their trigonometric identities. Form them into the Pythagorem theorem.
Then divide the whole equation by R which causes all the R’s to cancel out.
The following equation has been reduced
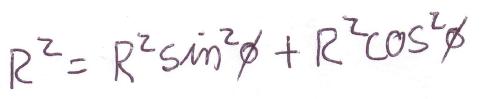
Solving Identity
Cast out the R’s
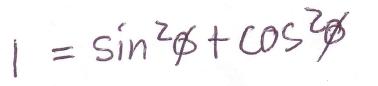
Casting out the R’s and Simplifying
Final Trigonometric Identity:
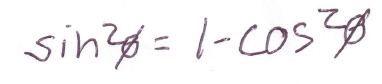
Simplified Trigonometric Identity
You may be wondering why we went through all this lengthy calculation, reduction and so forth. The reason for this process is to make us use our math, and secondly, not just to accept any old formula as truth, unless we can come up with it ourselves. This “coming up with” an equation is essential for good decision making and seperates the ammatures from the professionals.
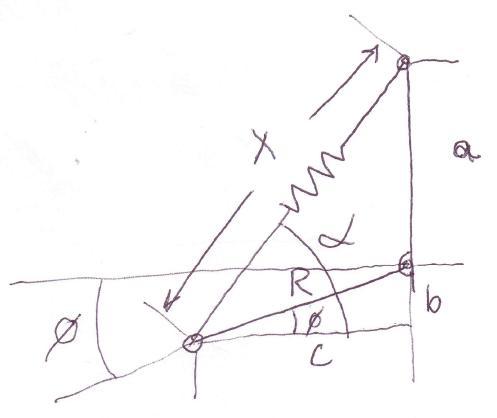
Suspension Mechanism: Next time we will discuss the how to analyze this mechanism with relative ease, using…you guessed it: trigonometry!
If you can derive an answer and back it up, you are alot farther ahead than if you just accepted an answer.
Next time will discuss the following suspension component and how to solve its movement using vector loop equations. We will be able to figure out how it moves very accurately, how much force is being exerted by the spring, how much load is being exerted at each joint and so forth.
And you guessed it…trigonometry is at the heart of its solution…



nice post. I would love to follow you on twitter.
You can follow us on twitter at GoKartGuru